数据结构与算法的复杂性分析

什么是复杂度分析（Complexity Analysis）？

复杂性分析被定义为一种根据输入大小（独立于机器、语言和编译器）来表征算法所花费时间的技术。它用于评估不同算法的执行时间的变化。我们可以在程序运行之前，在程序编码阶段就进行代码时间复杂度和空间复杂度的估算，进而提高代码运行效率。

如何衡量复杂性？

算法的复杂性可以通过两种方式来衡量：

• 时间复杂度（Time Complexity）：衡量执行当前算法所消耗的时间，通常使用$T(n)=O(f(n))$来表示
• 空间复杂度（Space Complexity）：衡量执行当前算法所需要占用的存储空间，通常使用$S(n)=O(f(n))$来表示

时间复杂度的大O符号表示法

大O符号

大O符号（英语：Big O notation），又称为渐进符号，是用于描述函数渐近行为的数学符号。更确切地说，它是用另一个（通常更简单的）函数来描述一个函数数量级的渐近上界。

大O符号表示法并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势。时间复杂度使用大O符号表示法的公式表示为

$$T(n)=O(f(n))$$

其中：

• $n$表示数据规模的大小
• $f(n)$表示每行代码执行的次数总和
• $O$代表代码的执行时间$T(n)$与$f(n)$表达式成正比
• $T(n)$表示解决这一问题的某一算法最坏情况下所需要的执行时间

这个公式的的全称为：算法的渐进时间复杂度，它表示算法运行时间的上限，如图展示了几种常见的复杂度形式，X轴代表数据的大小或者说是规模，Y轴表示程序的运行时间也就是复杂度：

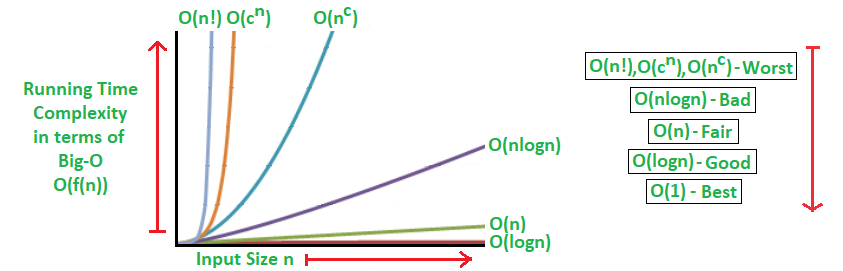
常见的时间复杂度

时间复杂度	阶	f(n) 举例
常数复杂度	$O(1)$	$1$
线性复杂度	$O(n)$	$n + 1$
对数复杂度	$O(logn)$	$logn + 1$
线性对数复杂度	$O(nlogn)$	$nlogn + 1$
K次方阶复杂度	$O(n^k)$、$O(n^2)$、$O(n^3)$...	$n^2 + n +1$
指数复杂度	$O(2^n)$	$2^n + 1$
阶乘复杂度	$O(n!)$	$n! + 1$

时间效率排名为（越靠右越代表算法的时间效率越低）:

$$O(1) < O(logn) < O(n) < O(n^2) < O(n^3) < O(2^n)$$

常数阶 $O(1)$

$O(1)$ 是常数时间复杂度，代码的执行时间不随n的变化而变化，例如在下面的代码中无论$n$的值有多大，代码执行时间都是一样的

int n = 50;
n = n * 2;
System.out.println(n);

线性阶 $O(n)$

$O(n)$ 是线性阶时间复杂度，代码的执行时间随着n的变化而变化，因此这类代码都可以用$O(n)$来表示它的时间复杂度。示例如下：

for (int i = 0; i < n; i++) {
    int x = i * 2;
    System.out.println(x);
}

对数阶 $O(logn)$

对数的定义

如果 $a^x=N$ （a>0，且a≠1），那么数$x$叫做以$a$为底$N$的对数，记作$x=log_aN$，读作以$a$为底$N$的对数，其中$a$叫做对数的底数，$N$叫做真数。

$O(logn)$ 是对数时间复杂度，示例如下，参数为n：

int m = 1;
while (m < n) {
    m = m * 2;
}

分析上面代码可知，在while循环里面，每次都将m乘以2，乘完之后，m距离n就越来越近了，推导可得 $m*2*2*...*2 \geq n$，假设m需要乘以x个2，m为常数1，x为循环次数，那么相当于求$2^x=n$，得$x=log_2n$，由于存在对数的换底公式，对数的底对于复杂度没有影响，所以算法的复杂度也就是$O(logn)$

线性对数阶 $O(nlogn)$

$O(nlogn)$是线性对数阶时间复杂度，它非常容易理解，将时间复杂度为 $O(logn)$ 的代码循环n遍的话，那么它的时间复杂度就是 $n*O(logn)$，也就是 $O(nlogn)$，示例如下，

for (int i = 0; i < n; i++) {
    int m = 1;
    while (m < n) {
        m = m * 2;
    }
}

k次方阶 $O(n^k)$

$O(n^k)$ 是k次方阶时间复杂度，平方阶、立方阶同理，把 $O(n)$ 的代码嵌套循环k遍就是k次方阶时间复杂度，嵌套循环2次的平方阶$O(n^2)$示例如下

for (int i1 = 0; i1 < n; i1++) {
    for (int i2 = 0; i2 < n; i2++) {
        int x = i2 * 2;
        System.out.println(x);
    }
}

如果平方阶将其中一层循环的n改成 m，那它的时间复杂度就变成了O(m x n)

指数阶 $O(2^n)$

$O(2^n)$ 是指数阶时间复杂度，随着数据规模的增长，算法的执行时间和空间占用会暴增，算法性能极差。一个简单的斐波那契数列递归示例如下：

//斐波那契数列
public static int exponentialFunctionTest(int n) {
    if (n <= 1) {
        return 1;
    } else {
        return exponentialFunctionTest(n - 1) + exponentialFunctionTest(n - 2);
    }
}

阶乘 $O(n!)$

$O(n!)$ 是阶乘时间复杂度，一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。自然数n的阶乘写作$n!$。

阶乘的复杂度，最典型的例子就是旅行推销员问题，有兴趣可以看下。

简单示例如下：

public static void factorial(int n) {
    for (int i = 0; i < n; i++) {
        factorial(n - 1);
    }
}

上面例子中循环执行次数最多的语句为factorial(n - 1)，在当前$n$下，会调用$n$次factorial(n - 1)，而在每个$n−1$下，又会调用$n-1$次factorial(n - 2)，以此类推，得执行次数为 $n × ( n − 1 ) × ( n − 2 ) × . . . × 1$，即$n!$。

参考资料

• https://www.geeksforgeeks.org/complete-guide-on-complexity-analysis/
• https://www.cnblogs.com/linj7/p/14133072.html
• https://zhuanlan.zhihu.com/p/143358017
• https://zhuanlan.zhihu.com/p/50479555